From Pringles® to Space - Unveiling the Mysteries of Hyperbolic Paraboloids and Magic Linear Structures
Recently, I stumbled upon an intriguing post by Alex Wang that sheds light on the fascinating origin of Pringles®’ shape.
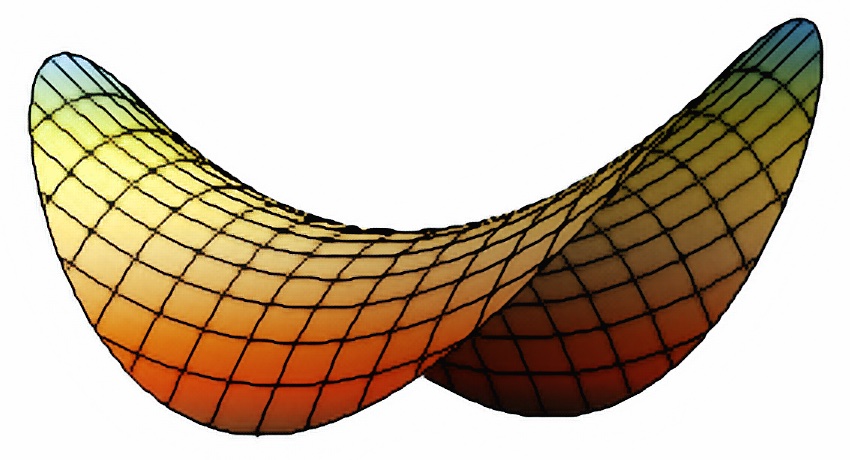
It turns out that this iconic snack isn’t just a happy accident – it’s actually a product of mathematics, specifically a second-order surface type known as the hyperbolic paraboloid, which happens to resemble a “saddle”. So, let’s saddle up and explore the mathematical magic behind Pringles®!
The original post by Alex:
⚡️ Let’s add a bit more scientific boredom!
Aside from being a mouthful to say, the hyperbolic paraboloid is an incredible geometric shape, and it happens to be a ruled surface. In simpler terms, it’s a surface created by the movement of a straight line (Fig. 1). Here we have points on two circles, connected with straight lines. Rotating the lower circle, we get hyperboloid of one sheet and then a cone. Parameter \(t\) is the angle by which we rotate the lower circle. Such models can be seen in some museums. Equation is:
\[x^{2}+y^{2}=1+(z^{2}-1)\sin ^{2}{t \over 2}, t = 0..2\pi.\]
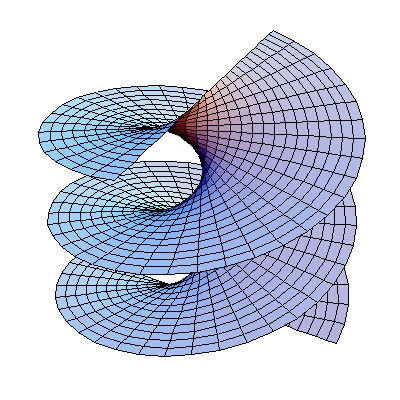
Ruled surfaces include cylinders, hyperboloids, cones, etc (Fig. 2). But this isn’t just about geeking out over geometry; it’s about Architectural and Engineering dynamite!
⚡️ Architectural dynamite
Parabolic and linear surfaces have found a unique application in architecture, thanks to their ability to create efficient structures with impressive architectural aesthetics (Lauriola, 2017). Parabolic curves can provide rational or optimal load distribution and perfect utilization of natural light, while linear surfaces add elements of geometric complexity and visual depth to modern buildings, transforming them into true architectural masterpieces.
Take a look at these masterpieces:

(Moscow, Russia)

(Guangzhou, China)

(Kobe, Japan)

(Ciechanow, Poland)

(Barcelona, Spain)

(Warsaw, Poland)
But wait, there’s more!
⚡️ Engineering dynamite
This same principle underpins the structural designs of space rockets.
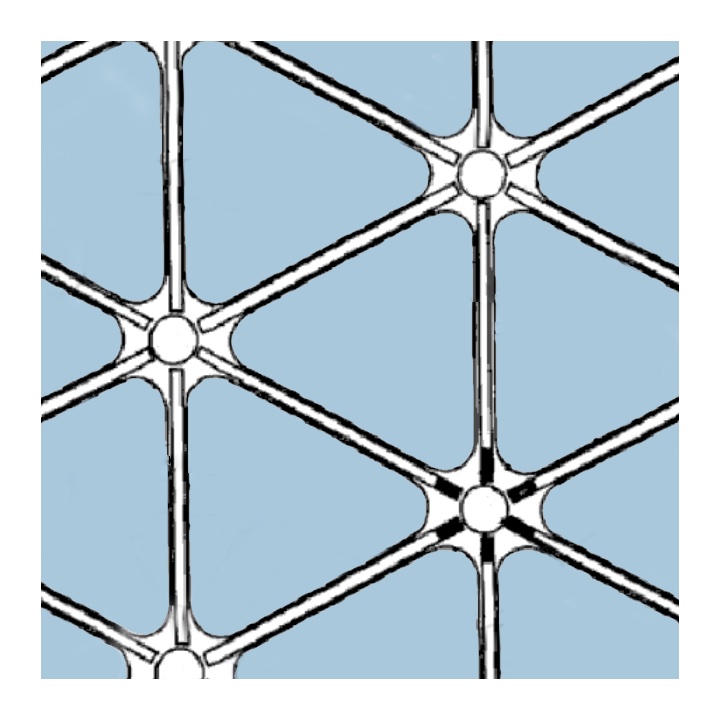
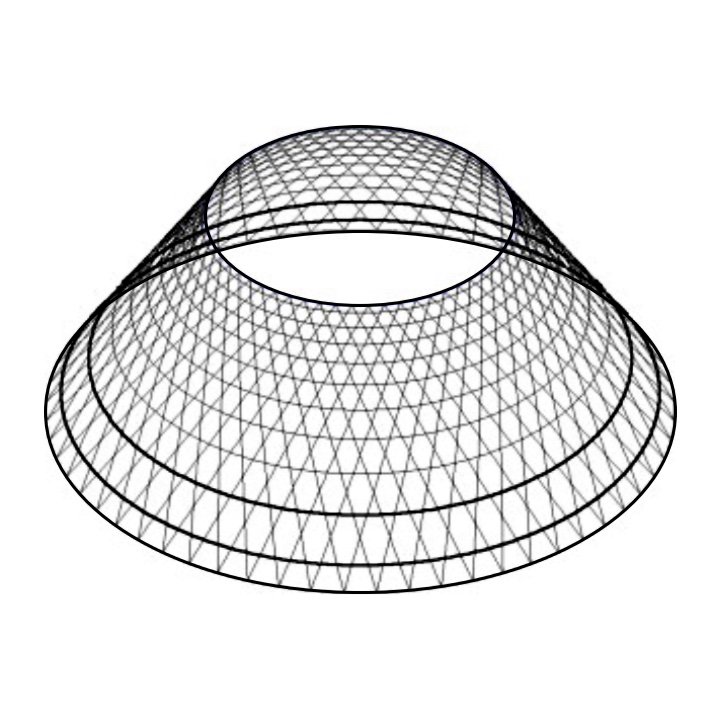
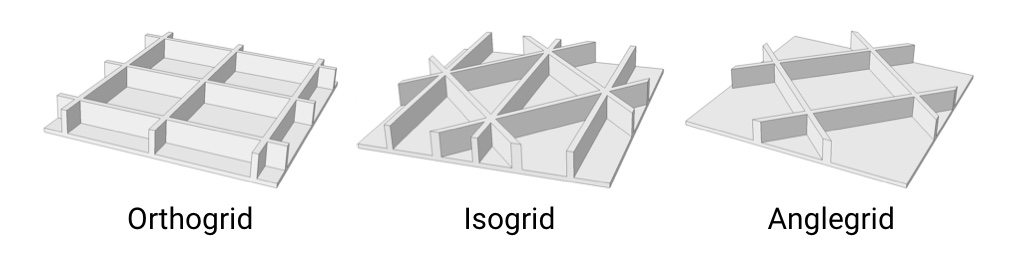
During the space race, both the USSR and the USA were pioneering various technologies for manufacturing grid-like structural components for rockets and spacecraft. For instance, McDonnell Douglas (now part of Boeing) patented isogrid structures (Fig. 9 - 10). See patent US4012549A (Slysh, 1977). Orthogrid and angle-grid structures also came into existence (Fig. 11). These designs have been and continue to be utilized in rockets like the “Atlas”, “Delta” and even in the “Crew Dragon” spaceship.


However, in my view, significant breakthroughs occurred in the 1980’s at the CRISM institute (USSR/Russia). There, anisogrid structures were developed and patented – high-strength composite structures created by winding continuous carbon fibers (CFRP). Such structures serve as the primary load-bearing components in the payload adapters of modern “Proton” class rockets (Fig. 12). They exhibit tremendous weight efficiency and stability (Vasiliev et al., 2009).

Just search for “anisogrid structure” and prepare to be amazed!
⚡️ Accessories
And if you want a ruled surface as a personal accessory, just use a Vietnamese hat made of leaves known as “Nón lá” (Fig. 13).